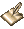I've only run across that projection the context of environment mapping before, and those maps are usually missing corners because of how they are defined (look a couple of pages down in http://download.nvidia.com/developer...EnvMapping.pdf for some examples).
I therefore need to ask: how did you get it into the dual paraboloid projection? And are you sure that this really is a dual paraboloid projection? It looks more like a cubemap than anything else I could come up with. A bit of quick pasting in Photoshop shows beautiful alignment across map edges when one hemisphere is aligned and rotated with respect to the other, meaning that it's much more likely a toroid of some sort. My best guess would be that if you printed it out and folded it back on itself then the edges would perfectly line up without any distortion.
If it indeed originated as a pair (or more) of flat maps, then you're going to get some significant distortion converting it to equirectangular. One way to make the distortions less unpleasant might be to put the poles into the corners and then go for something like an octahedral environment map. Depending on how much distortion you can tolerate, the Peirce Quincuncial projection might work for preserving conformality, but would require a 45 degree rotation of your image after slicing and rearrangement as well as suffering significant distortions in area for some locations. However, it turns out that your image has convenient oceans in the singularity points (this one was tiled, rotated, and very sloppily cropped after eyeballing the center):
Jemison_Color copysmall_b.jpg
Assuming that the original map is really a piecewise-linear set of things, you can split that map into the 16 triangles on the above image and map those to a sphere using a 3D modeling tool like Blender (should be just as easy from the original as from the rotated one I used). I'll try to remember to write a quick-and-dirty mapper, but I don't know when I'll get around to it.








 Reply With Quote
Reply With Quote